Gradient Similarity Surgery in Multi-task Deep Learning

Thomas Borsani 1
Andrea Rosani 1
Giuseppe Nicosia 2
Giuseppe Di Fatta 1

ECML PKDD 2025

1Free University of Bozen-Bolzano, 2University of Catania

Code arXiv

Abstract

The multi-task learning (MTL) paradigm aims to simultaneously learn multiple tasks, within a single model, capturing higher-level, more general hidden patterns that are shared by the tasks. In deep learning, a significant challenge in the backpropagation training process is the design of advanced optimisers to improve the convergence speed and stability of the gradient descent learning rule. In particular, in multi-task deep learning (MTDL) the multitude of tasks may generate potentially conflicting gradients that would hinder the concurrent convergence of the diverse loss functions. This challenge arises when the gradients of the task objectives have either different magnitudes or opposite directions, causing one or a few to dominate or to interfere with each other, thus degrading the training process. Gradient surgery methods address the problem explicitly dealing with conflicting gradients by adjusting the overall gradient trajectory. This work introduces a novel gradient surgery method, the Similarity-Aware Momentum Gradient Surgery (SAM-GS), which provides an effective and scalable approach based on a gradient magnitude similarity measure to guide the optimisation process. The SAM-GS surgery adopts gradient equalisation and modulation of the first-order momentum. A series of experimental tests have shown the effectiveness of SAM-GS on synthetic problems and MTL benchmarks. Gradient magnitude similarity plays an important role in regularising gradient aggregation in MTDL for the optimisation of the learning process.

Methods

The proposed approach focuses solely on magnitude gradient conflicts, which are arguably the most critical impediment to effective MTDL optimisation.
Angle-based gradient conflicts are intentionally disregarded, as they primarily affect convergence speed rather than convergence feasibility.

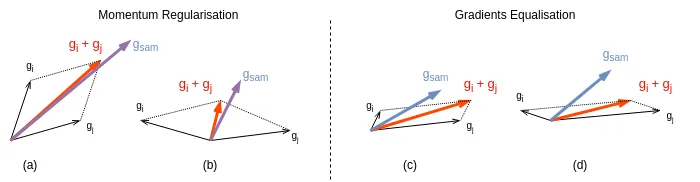
Let us examine why angle-based gradient conflicts may slow down convergence, while magnitude gradient conflicts can severely hinder the overall optimisation process—potentially preventing certain tasks from converging altogether.

When adding two task gradients gi\mathbf{g}_i and gj\mathbf{g}_j of similar magnitude (∣gi∣≃∣gj∣|\mathbf{g}_i| \simeq |\mathbf{g}_j|), but with an angle α>90∘\alpha > 90^{\circ} between them, the magnitude of their sum is reduced due to destructive interference. Specifically, the resultant magnitude is scaled by a factor proportional to cos⁡(α)\cos(\alpha), as illustrated in Figures a and b.
In the worst-case scenario (α=180∘\alpha = 180^\circ) the gradients point in exactly opposite directions and cancel each other out. However, such extreme angular conflicts are rare in practice. Even when partially cancelling, the resulting vector still encodes meaningful optimisation direction, which can be amplified by first-order momentum mechanisms without explicitly resolving the angle conflict.

In contrast, when one task’s gradient is significantly larger than the others (∣gi∣≫∣gj∣|\mathbf{g}_i| \gg |\mathbf{g}_j|), the aggregated gradient direction becomes dominated by that task. This is much more harmful, as it biases the optimisation process toward a single objective, effectively stalling learning for other tasks (see Figure c).

Illustration of four scenarios for two task gradients, gi and gj, the standard overall gradient is denoted as gi + gj and the overall gradient of SAM-GS is denote as gSAM. (a) Ideal case: Gradients have similar magnitudes, and the angle between them is less than 90◦, indicating no conflict. (b) angle-based gradient conflict: The angle between gradients exceeds 90◦, diminishing the effectiveness of their combination. (c) magnitude-based gradient conflict: One gradient dominates, leading to an imbalanced gradient update. (d) Both conflicts: A combination of angle- and magnitude-based gradient conflicts, where both the directional misalignment and magnitude disparity hinder effective gradient aggregation.
IIllustration of four scenarios for two task gradients, gi and gj, the standard overall gradient is denoted as gi + gj and the overall gradient of SAM-GS is denote as gSAM. (a) Ideal case: Gradients have similar magnitudes, and the angle between them is less than 90◦, indicating no conflict. (b) angle-based gradient conflict: The angle between gradients exceeds 90◦, diminishing the effectiveness of their combination. (c) magnitude-based gradient conflict: One gradient dominates, leading to an imbalanced gradient update. (d) Both conflicts: A combination of angle- and magnitude-based gradient conflicts, where both the directional misalignment and magnitude disparity hinder effective gradient aggregation.

Synthetic Problem

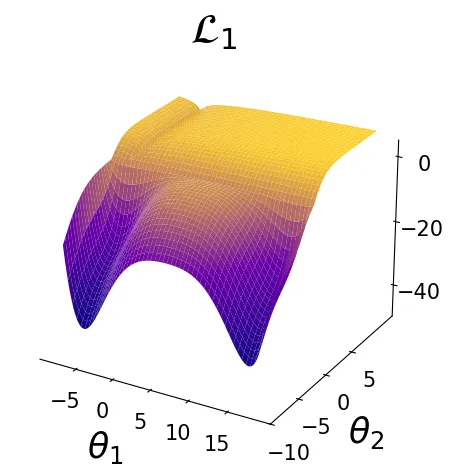
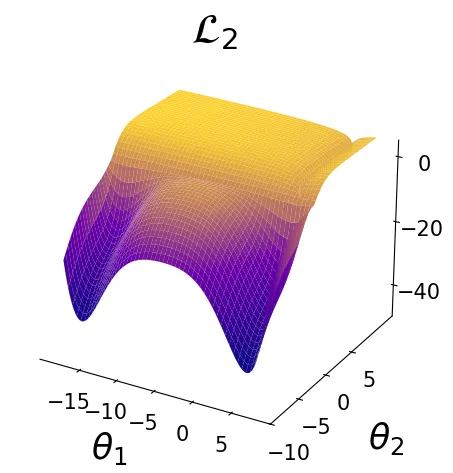
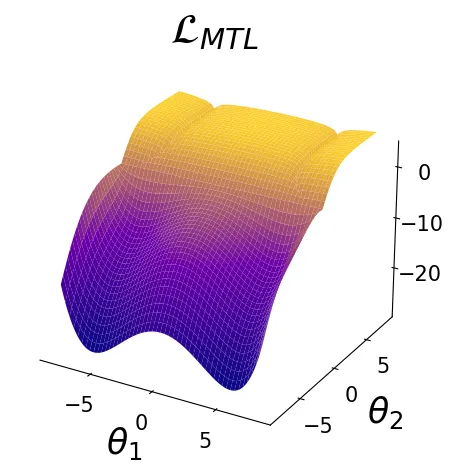
To illustrate the gradient surgery problem in a simplified setting, we adopt the 2D multi-task optimisation problem proposed in Nash-MTL (Navon et al. 2022). This problem provides a controlled environment for the study of conflicting gradient across tasks, highlighting the challenges of multi-task optimisation. In addition, we introduce a novel variant of that problem with a similar loss landscape structure, featuring two global minima, providing a different problem setting to analyse the impact of multiple optima on optimisation dynamics.

Illustration of the multi-task optimisation problem with two loss function with one optimal solution and the MTL problem computed as the sum of two losses.

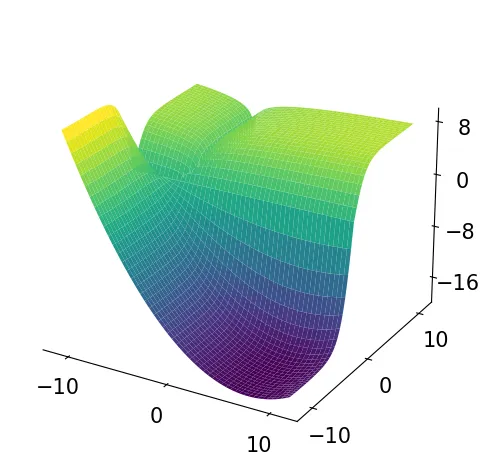
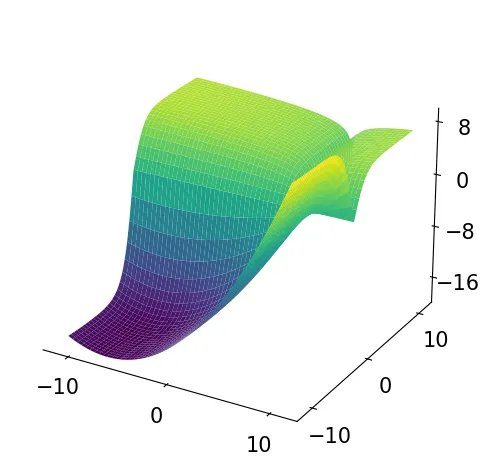
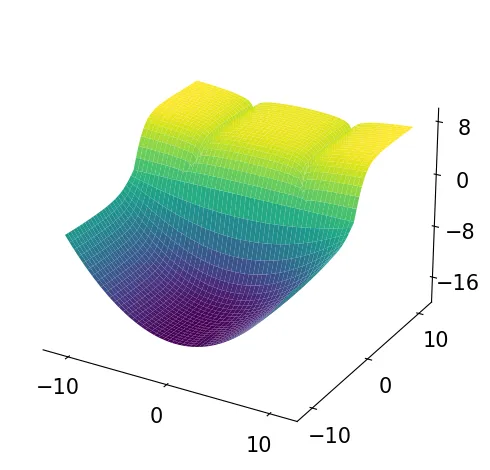
Illustration of the multi-task optimisation problem with two loss function with one optimal solution and one local optima solution. The MTL problem computed as the sum of two losses.

Algorithm

BibTeX citation

    @misc{borsani2025gradientsimilaritysurgerymultitask,
      title={Gradient Similarity Surgery in Multi-Task Deep Learning}, 
      author={Thomas Borsani and Andrea Rosani and Giuseppe Nicosia and Giuseppe Di Fatta},
      year={2025},
      eprint={2506.06130},
      archivePrefix={arXiv},
      primaryClass={cs.LG},
      url={https://arxiv.org/abs/2506.06130}, 
}